
In that sense we could consider the generated networks in this research as potential supply networks, corresponding to companies from medium to very large size. However, considering some extreme cases will provide additional understanding of the subject and facilitate the identification of the behaviour of each factor over the objective variable. This might generate some supply networks that appear unrealistic when compared to real life networks. It is important to note that to analyse the influence of the various factors under consideration, it is necessary to define different levels for each factor. As an example, Figure 1 represents two of the 81,920 network structures generated according to the factors of the experiment. Furthermore, each of the suppliers will be responsible for the shipment of one type of raw material required for the finished product. Each of the elements of the network (nodes, clusters and flows) will have an associated reliability, which is the probability that it will function without disruption when required (in the case of a cluster, a disruption would affect all the nodes in the region associated to that cluster).
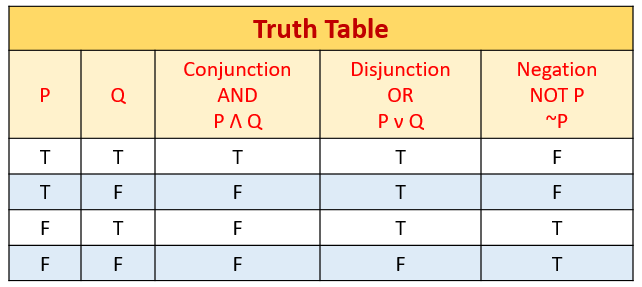
Given that one of the factors under analysis is the clusterisation (density) of nodes around a particular region, each warehouse is assigned to a region, for which the number of nodes assigned to it will define the density of the cluster. In this context, a certain supply network will be represented by a set of nodes (suppliers, warehouses and final customers) linked together by arrows representing the flow (transport) of products between the nodes. To analyse the reliability of man-made networks – not only supply networks, but also others such as telecom networks and social networks – modelling is usually represented using graphs (Asha and Newth, 2007). All statistical analysis was carried out with the statistical package R. Given that it is possible that different raw materials are used, the output variable will be the product of the reliabilities obtained for each product, considering that all raw materials should reach the final customer. All the factors are fixed and the model includes second order interaction terms. We conducted a balanced 2 13 full-factorial design with ten replicates, giving a total of 81,920 observations. A multi-factorial Design of Experiments (DOE) was thus performed to test differences between factors (and the presence of interactions between them) when observing the resulting supply network reliabilities. Hence a total of 13 factors have been considered, each at two levels (Table I), as usually done in exploratory analysis (Eriksson et al. Finally, we have also taken into consideration the variances in reliability of four of the variables: density variance (F5) node variance (F11), flow variance (F12) and cluster variance (F13), which could affect overall reliability. Second, we included the reliabilities of specific nodes (F8), flows (F9), and clusters (F10), as it would be expected that more reliable components would make more reliable networks. The implication is true in all other cases. aĪn implication is false if the first operand is true while the second operand is false. Two expressions are equivalent if they result in the same truth value. Another way to think about it is that the result is true if the two operands have different values, otherwise the result is false. aĮxclusive or is similar to the or operator with the only difference being that the result is false if both operands are true. The result is only false if both operands are false. The result of the or operator is true if at least one of the operands are true. If one or both of the operands are false the result is false. The and operator is a binary operator that results in true if both operands are true. This means that true becomes false, and false becomes true. The not operator is used to negate an expression. It can also be used to compare two different expressions by showing them side-by-side in the same table. Truth tables often makes it easier to understand the Boolean expressions and can be of great help when simplifying expressions. True:Ī truth table shows the evaluation of a Boolean expression for all the combinations of possible truth values that the variables of the expression can have. If an expression contains a word that is not listed it will instead be treated as a variable.

The following table lists all the symbols that the tool recognizes and shows for what purpose they are used. There are many different ways to write the same expression. The basic operators are and, or and not (negation), from which all other operators can be derived. A Boolean expression is an expression consisting of variables and truth values ( true and false) connected with various logical operators.


 0 kommentar(er)
0 kommentar(er)
